ฟังก์ชัน

                ฟังก์ชัน เป็นบทเรียนที่ต่อจากเรื่องความสัมพันธ์ ในบทเรียนนี้จะได้รู้จักว่าฟังก์ชันเป็นอย่างไร มีเงื่อนไขอย่างไร การแทนฟังก์ชัน ฟังก์ชันจาก Aไป B ฟังก์ชันที่ควรรู้จัก พร้อมทั้งนำไปประยุกต์ใช้ในการแก้สมการและอสมการ การแก้โจทย์ปัญหาฟังก์ชัน ฟังก์ชันคอมโพสิท ฟังก์ชันอินเวอร์ส และพีชคณิตของฟังก์ชัน อ่านเพิ่มเติม

ฟังก์ชันเชิงเส้น

           ฟังก์ชันเชิงเส้น คือ ฟังก์ชันที่อยู่ในรูป f(x) = ax+b เมื่อ a และ b เป็นจำนวนจริงเช่น f(x) = 2x+1
f(x) = -3x f(x) = x-5 เป็นต้น กราฟของฟังก์ชันเหล่านี้เป็นเส้นตรงที่ไม่ขนานกับแกน ฟังก์ชันเชิงเส้น f(x) = ax+b เมื่อ a=0 จะได้ฟังก์ชันอยู่ในรูป f(x) = b ฟังก์ชันนี้มีชื่อเรียกเฉพาะว่า ‘‘ ฟังก์ชันคงตัว ’’ (Constant function) กราฟของฟังก์ชันคงตัวจะเป็นเส้นตรงที่ขนานกับแกน x เช่น f(x) = 4 , f(x) = -2 เป็นต้น อ่านเพิ่มเติม

ฟังก์ชันกำลังสอง

             กราฟของฟังก์ชันกำลังสอง มีชื่อเรียกว่า พาราโบลา ซึ่งลักษณะของกราฟของฟังก์ชันขึ้นอยู่กับค่าของ a , b และ c และเมื่อ a เป็นบวกหรือลบ จะทำให้ได้กราฟเป็นเส้นโค้งหงายหรือคว่ำ และกราฟของฟังก์ชันกำลังสองที่กำหนดด้วยสมการ y = ax^2 เมื่อ a ไม่เท่ากับ 0 เมื่อ a > 0 และชนิดคว่ำ เมื่อ a < 0 อ่านเพิ่มเติม

ฟังก์ชันเอกซ์โพเนนเชียล

            เรียก an ว่า เลขยกกำลัง เรียก a ว่าฐานของเลขยกกำลัง และ เรียก n ว่าเลขชี้กำลัง
เลขยกกำลังที่มีเลขชี้กำลังเป็นจำนวนเต็ม มีสมบัติตามทฤษฎีบทต่อไปนี้ อ่านเพิ่มเติม

ฟังก์ชันค่าสัมบูรณ์

        ฟังก์ชันค่าสมบูรณ์ ถูกกำหนดโดยกฎซึ่งแบ่งออกเป็นสองกรณี
ค่าฟังก์ชันสมบูรณ์ | | จะกำหนดโดย



ค่า absolute ของ x ให้ระยะห่างระหว่าง x และ 0 เป็นบวกหรือศู อ่านเพิ่มเติม

ฟังก์ชันขั้นบันได

               ฟังก์ชันขั้นบันได คือฟังก์ชันบนจำนวนจริงซึ่งเกิดจากการรวมกันระหว่างฟังก์ชันคงตัวจากโดเมนที่แบ่งออกเป็นช่วงหลายช่วง กราฟของฟังก์ชันจะมีลักษณะเป็นส่วนของเส้นตรงหรือรังสีในแนวราบเป็นท่อน ๆ ตามช่วง ในระดับความสูง อ่านเพิ่มเติม

โดเมนและเรนจ์

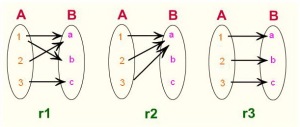
เซตของสมาชิกตัวหน้าในคู่อันดับของ r1 = {1,2,3,4} เรียกเซตนี้ว่า โดเมนของ r1
เซตของสมาชิกตัวหลังในคู่อันดับของ r1 = {2,3,4,5} เรียกเซตนี้ว่า เรนจ์ของr1
ส่วนใน r2 จะเห็นว่าโดเมนของ r2 เท่ากับเรนจ์ของ r2 คือเซตของจำนวนเต็ม อ่านเพิ่มเติม

ความสัมพันธ์

           คู่อันดับ (Order Pair) เป็นการจับคู่สิ่งของโดยถือลำดับเป็นสำคัญ เช่น คู่อันดับ a, b จะเขียนแทนด้วย (a, b) เรียก a ว่าเป็นสมาชิกตัวหน้า และเรียก b ว่าเป็นสมาชิกตัวหลัง
(การเท่ากับของคู่อันดับ) (a, b) = (c, d) ก็ต่อเมื่อ a = c และ b = d
          ผลคูณคาร์ทีเชียน (Cartesian Product) ผลคูณคาร์ทีเซียนของเซต A และเซต B คือ เซตของคู่อันดับ (a, b) ทั้งหมด โดยที่ a เป็นสมาชิกของเซต A และ b เป็นสมาชิกของเซต B
สัญลักษณ์ ผลคูณคาร์ทีเซียนของเซต A และเซต B เขีย อ่านเพิ่มเติม